UCT(Upper Confidence Boundary of Tree)에 대한 정확한 정리

이전 포스팅 '몬테카를로 트리 서치 (Monte Carlo Tree Search)에 대한 정확한 정리'에서 tree policy를 다루었습니다.

Tree policy는 선택(Selection) 단계에서 확장(Expansion)을 이어나갈 child node를 선택할 때 사용하는 정책이며,

알파고의 경우 이용(exploitation)과 탐사(exploration)의 균형을 맞추어 이용-탐사 딜레마를 해결하기 위해 tree policy로 UCT(Upper Confidence Boundary of Tree)가 사용되었고,

UCT는 UCB1(Upper Confidence Boundary)이 tree에 사용되었다고 해서 붙은 이름이라는 것이 지난 포스팅의 내용이었습니다.

우선 아래 그림을 통해 UCB1을 이해해 보겠습니다.

출처 : 오츠키 토모시, 정인식 역, 알파고를 분석하며 배우는 인공지능, 제이펍, 2019 http://www.kocw.net/home/search/kemView.do?kemId=1367683

 

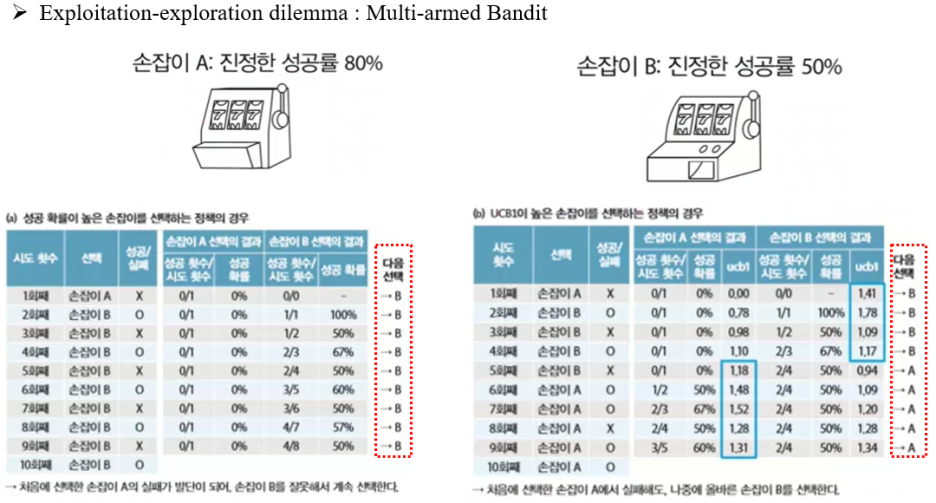
'알파고를 분석하며 배우는 인공지능' 책에서 참고한 그림입니다. 캡쳐는 이 책을 교재로 사용한 강의를 kocw 사이트에 찾아서 해온 것인데, 정말 좋은 책이니 시간 되시면 꼭 읽어보시길 추천합니다. 강의도 들으시면 더 좋을 것입니다.

이용-탐사 딜레마는 Multi-armed Bandit 문제에서 비롯되었습니다. MCTS와 관련된 논문을 읽다보면 자주 볼 수 있는 예시로, 보통 UCB1 알고리즘을 설명하기 위한 목적으로 등장합니다.

Multi-armed bandit 문제는 두 개의 슬롯 머신이 있을 때 발생할 수 있는 문제로, 위에서 보시다시피 당장의 승률만을 기반으로 슬롯 머신를 선택하면 왼쪽 표처럼 A 슬롯 머신은 아예 선택되지도 못하고 B 슬롯 머신만 계속 선택하게 됩니다.

A 슬롯 머신의 승률(80%)이 B 슬롯 머신의 승률(50%)보다 높은데도 말이죠.

 

하지만 승률이 아닌 선택된 횟수도 고려하여 슬롯 머신을 선택하면, 오른쪽 표처럼 A 슬롯 머신을 선택하는 바람직한 결과가 도출됩니다.

승률과 함께 선택 횟수도 함께 고려한 알고리즘이 UCB1 알고리즘으로, 수식으로 나타내면 아래와 같습니다.

 

왼쪽 항 \( \bar X_{j} \)는 임의의 child node \( {j} \)의 평균 보상을 의미하는 [0, 1] 사이의 값으로, 게임의 경우 승률에 해당합니다. 

오른쪽 항 \( \sqrt{{ 2\ln(n) \over n_{j} }} \)의 \( n_{j} \)는 child node \( {j} \)의 방문 횟수, \( {n} \)은 그것의 parent node의 방문 횟수입니다.

\( n_{j} \)가 분모에 있으므로  child node \( {j} \)의 방문 횟수가 작아지면 \( \bar X_{j} \) 값(게임의 경우 승률)이 작아도 \( \sqrt{{ 2\ln(n) \over n_{j} }} \) 값이 커지므로, 해당 node의 전체적인 UCB1 값이 커져서 선택될 확률이 높아집니다.

아래 수식이 바로 UCB1을 기반으로 만들어진 UCT의 수식입니다. MCTS는 이 UCT를 tree policy로 채택하여, 한 번도 선택되지 않는 leaf node가 발생하지 않게 합니다.

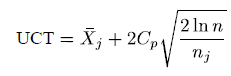
UCT 수식에서 UCB1과의 차이점은 \( C_{p} \)이라는 항이 추가된 것입니다. 이 값을 조절해서 탐사를 적게 하거나, 많이 하도록 할 수 있습니다. 많은 시뮬레이션을 통해 조절되는 값이라 볼 수 있습니다.

\( C_{p} \) 값을 크게 하면 오른쪽 항의 증가 폭이 더 커져서 탐사되는 횟수가 많아집니다. 게임의 종류에 따라 조절되는 값으로, 알파고에서는 \( \sqrt2 \)가 사용되었습니다.

 

이상으로 알파고에서 MCTS의 tree policy로 사용된 UCT를 알아보았습니다. 감사합니다.